Защита программ и забывающее моделирование на ram-машинах
Основные положения
В этом разделе рассматриваются теоретические аспекты защиты программ от копирования. Эта задача защиты сводится к задаче эффективного моделирования RAM-машины (машины с произвольным доступом к памяти []) посредством забывающей RAM-машины. Следует заметить, что основные результаты по данной тематике (их можно получить на соответствующем личном интернетовском сайте) принадлежат О. Голдрайху и Р. Островски и эти исследования активно продолжаются в настоящее время.
Машина является забывающей, если последовательность операций доступа к ячейкам памяти эквивалентна для любых двух входов с одним и тем же временем выполнения. Например, забывающая машина Тьюринга - это машина, для которой перемещение головок по лентам является идентичным для каждого вычисления и, таким образом, перемещения не зависят от фактического входа.
Необходимо выделить следующую формулировку ключевой задачи изучения программы по особенностям ее работы. "Как можно эффективно моделировать независимую RAM-программу на вероятностной забывающей RAM-машине". В предположении, что односторонние функции существуют, далее показывается, как можно сделать некоторую схему защиты программ стойкой против полиномиально-временного противника, которому позволено изменять содержимое памяти в процессе выполнения программы в динамическом режиме.
Центральный процессор, имитирующий взаимодействие. Неформально, будем говорить, что центральный процессор имитирует взаимодействие с соответствующими зашифрованными программами, если никакой вероятностный полиномиально-временной противник не может различить следующие два случая, когда по данной зашифрованной программе как входу:
-
противник экспериментирует с оригинальным защищенным ЦП, который пытается выполнить зашифрованную программу, используя память;
противник экспериментирует с "поддельным" (фальсифицированным) ЦП. Взаимодействия поддельного ЦП с памятью почти идентичны тем, которые оригинальный ЦП имел бы с памятью при выполнении фиксированной фиктивной программы.
Выполнение фиктивной программы не зависит по времени от числа шагов реальной программы. Не зависимо от времени поддельный ЦП (некоторым "волшебным" образом) записывает в память тот же самый выход, который подлинный ЦП написал, выполняя "реальную" программу.
При создании ЦП, который имитирует эксперименты, имеются две проблемы. Первая заключается в том, что необходимо скрывать от противника значения, сохраненные и восстановленные из памяти, и предотвращать попытки противника изменять эти значения. Это делается с использованием традиционных криптографических методов (например, методов вероятностного шифрования и аутентификации сообщений). Вторая проблема заключается в необходимости скрывать от противника последовательность адресов, к которым осуществляется доступ в процессе выполнения программы (здесь и далее это определяется как сокрытие модели доступа).
Сокрытие оригинальной модели доступа к памяти - это абсолютно новая проблема и традиционные криптографические методы здесь не применимы. Цель в таком случае состоит в том, чтобы сделать невозможным для противника получить о программе что-либо полезное из модели доступа. В этом случае ЦП не будет выполнять программу обычным способом, однако он заменяет каждый оригинальный цикл "выборки/запоминания" многими циклами "выборки/запоминания". Это будет "путать" противника и предупреждать его от "изучения" оригинальной последовательности операций доступа к памяти (в отличие от фактической последовательности). Следовательно, противник не может улучшить свои способности по восстановлению оригинальной программы.
Ценой, которую необходимо заплатить за защиту программ, таким образом, является быстродействие вычислений. Неформально говоря, затраты на защиту программ определяются как отношение числа шагов выполнения защищенной программы к числу шагов исходного кода программы. Далее показывается, что эти затраты полиномиально связаны с параметром безопасности односторонней функции, что подтверждается следующим тезисом.
В то же время, простой комбинаторный аргумент показывает, что любое забывающее моделирование независимой RAM-машины должно иметь среднее число ?(lоgt) затрат. В связи с эти приводится следующий аргумент.
Пусть машина RAM(m) - определена как показано выше. Тогда каждое забывающее моделирование RAM(m)-машины должно содержать не менее max{m,(t-1)log m} операций доступа, чтобы смоделировать t шагов оригинальной программы.
Далее рассмотрим сценария наихудшего случая, в котором наблюдатель (или в данном случае противник) активно пытается получить информацию, вмешиваясь в процесс вычислений. Вопрос заключается в том, можно ли гарантировать, что воздействие противника является забывающим по входу. Неформально говоря, моделирование RAM-машины на забывающей RAM-машине является доказуемо защищенным от вмешательства, если моделирование остается забывающим (т.е. не вскрывает какой-либо информации о входе за исключением его длины) даже в случае, когда независимый "мощный" противник исследует и изменяет содержимое памяти. В связи с этим приводится следующий аргумент.
В условиях определения RAM(m)-машины t шагов независимой RAM(m)-программы могут быть промоделированы (доказуемо защищенным от вмешательства способом) менее чем за O(t(log2t)3) шагов на забывающей машине RAM(m(log2m)2).
Необходимо отметить, что вышеприведенные результаты относятся к RAM-машинам с доступом к случайному оракулу. Чтобы получить результаты для более реалистичных моделей вероятностных RAM-машин, необходимо заменить случайный оракул, используемый выше, псевдослучайной функцией. Такие функции существуют в предположении существования односторонних функций с использованием короткого действительно случайно выбранного начального значения.
Модели и определения
Далее рассматривается модель RAM как пара интерактивных машин с ограниченными ресурсами, и даются два базовых понятия: понятие защиты программ и понятие моделирования на забывающей RAM-машине.
RAM-машина как пара интерактивных машин. В данном разделе RAM-машина представляется как две интерактивные машины: центральный процессор (ЦП) и модуль памяти (МП).
Задача исследований сводится изучению взаимодействия между этими машинами. Для лучшего понимания необходимо начать с определения интерактивной машины Тьюринга.
Интерактивная машина Тьюринга - многоленточная машина Тьюринга, имеющая следующие ленты:
входная лента "только-для-чтения";
выходная лента "только-для-записи";
рабочая лента "для-записи-и-для-чтения";
коммуникационная лента "только-для-чтения";
коммуникационная лента "только-для-записи"
.
Под ITM(c,w) обозначается машина Тьюринга с рабочей лентой длины w и коммуникационными лентами, разделенными на блоки c-битной длины, которая функционирует следующим образом. Работа ITM(c,w) на входе у начинается с копирования у в первые |y| ячеек ее рабочей ленты. В случае если |y|>w, выполнение приостанавливается немедленно. В начале каждого раунда, машина читает следующий c-битный блок с коммуникационной ленты "только-для-чтения". После некоторого внутреннего вычисления, использующего рабочую ленту, раунд завершен с записью с битов на коммуникационную ленту "только-для-записи". Работа машины может завершиться в некоторой точке с копированием префикса ее рабочей ленты на выходную ленту машины. Теперь можно определить ЦП и МП как интерактивные машины Тьюринга, которые взаимодействуют друг с другом, а также можно ассоциировать коммуникационную ленту "только-для-чтения" ЦП с коммуникационной лентой "только-для-записи" МП и наоборот. Кроме того, и ЦП, и МП будут иметь ту же самую длину сообщений, то есть, параметр с, определенный выше. МП будет иметь рабочую ленту размером, экспоненциальным от длины сообщений, в то время как ЦП будет иметь рабочую ленту размером, линейным от длины сообщений. Каждое сообщение может содержать "адрес" на рабочей ленте МП и/или содержимое регистров ЦП.
Далее используем k как параметр, определяющий и длину сообщений, и размер рабочих лент ЦП и МП. Кроме того, длина сообщений будет равна k+2+k', а размер рабочей ленты будет равен 2kk', где k'=O(k).
Для каждого k
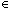 N определим MEMk как машину IТМ(k+2+O(k),2kO(k)), работающую точно так, как определено выше. Рабочая лента разбивается на 2k слов, каждое размером O(k). После копирования входа на рабочую ленту машина MEMk является машиной, управляемой сообщениями. После получения сообщения (i,a,v), где i
N определим MEMk как машину IТМ(k+2+O(k),2kO(k)), работающую точно так, как определено выше. Рабочая лента разбивается на 2k слов, каждое размером O(k). После копирования входа на рабочую ленту машина MEMk является машиной, управляемой сообщениями. После получения сообщения (i,a,v), где i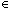
 {"запомнить","выборка","стоп"}, a
{"запомнить","выборка","стоп"}, a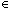
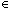 {0,1}O(k), машина MEMk работает следующим образом.
{0,1}O(k), машина MEMk работает следующим образом.Если i="запоминание", тогда машина MEMk копирует значение v из текущего сообщения в число а рабочей ленты.
Если i="выборка", тогда машина MEMk посылает сообщение, состоящее из текущего числа а (рабочей ленты).
Если i="стоп", тогда машину MEMk копирует префикс рабочей ленты (как специальный символ) на выходную ленту и останавливается.
Далее, пусть для каждого k
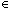 N определим CPUk как машину IТМ(k+2+O(k),O(k)), работающую точно так, как определено выше. После копирования входа на свою рабочую ленту, машина CPUk выполняет вычисления за время, ограниченное poly(k), используя рабочую ленту, и посылает сообщение, определенное в этих вычислениях. В следующих раундах CPUk - является машиной, управляемой сообщениями. После получения нового сообщения машина CPUk копирует сообщение на рабочую ленту и, основываясь на вычислениях на рабочей ленте, посылает свое сообщение. Число шагов каждого вычисления на рабочей ленте ограничено фиксированным полиномом от k.
N определим CPUk как машину IТМ(k+2+O(k),O(k)), работающую точно так, как определено выше. После копирования входа на свою рабочую ленту, машина CPUk выполняет вычисления за время, ограниченное poly(k), используя рабочую ленту, и посылает сообщение, определенное в этих вычислениях. В следующих раундах CPUk - является машиной, управляемой сообщениями. После получения нового сообщения машина CPUk копирует сообщение на рабочую ленту и, основываясь на вычислениях на рабочей ленте, посылает свое сообщение. Число шагов каждого вычисления на рабочей ленте ограничено фиксированным полиномом от k.Единственная роль входа ЦП должна заключаться в инициализации регистров ЦП, и этот вход может игнорироваться при последовательном обращении. "Внутреннее" вычисление ЦП в каждом раунде соответствует элементарным операциям над регистрами. Следовательно, число шагов, принимаемых в каждом таком вычислении является фиксированным полиномом от длины регистра (которая равна O(k)). Теперь можно определить RAM-модель вычислений, как совокупность RAMk-машин для каждого k.
Для каждого k
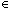 N определим машину RAMk как пару (CPUk, MEMk), где ленты "только-для-чтения" машины CPUk совпадают с лентами "только для записи" машины MEMk, а ленты "только-для-записи" машины CPUk совпадают с лентами "только-для-чтения" машины MEMk.
N определим машину RAMk как пару (CPUk, MEMk), где ленты "только-для-чтения" машины CPUk совпадают с лентами "только для записи" машины MEMk, а ленты "только-для-записи" машины CPUk совпадают с лентами "только-для-чтения" машины MEMk.Вход RAMk - это пара (s,y), где s - вход (инициализация) для CPUk и у - вход для MEMk. Выход машины RAMk по входу (s,у), обозначаемый как RAMk(s,у), определен как выход MEMk(y) при взаимодействии с CPUk(s).
Для того, чтобы рассматривать RAM-машину как универсальную машину, необходимо разделить вход у машины MEMk на "программу" и "данные". То есть, вход у памяти разделен (специальным символом) на две части, названные программой (обозначенной П) и данными (обозначаемыми x).
Пусть RAMk и s фиксированы и у=(П,х). Определим выход программы П на входных данных х, обозначаемый через П(x) как RAMk(s,у). Определим время выполнения П на данных х, обозначаемое через tП(x), как сумму величины (|у|+|П(x)|) и числа раундов вычисления RAMk(s,у). Определим также размер памяти программы П для данных х, обозначаемый через sП(x) как сумму величины |у| и числа различных адресов, появляющихся в сообщениях, посланных CPUk к MEMk в течение работы RАМk(s,у).
Легко увидеть, что вышеупомянутая формализация непосредственно соответствует модели вычислений с произвольным доступом к памяти. Следовательно, "выполнение П на х" соответствует раундам обмена сообщениями при вычислении RAMk(',(П,х)). Дополнительный член |y| + |П(x)| в tП(x) поясняет время, потраченное при чтении входа и записи выхода, в то время как каждый раунд обмена сообщениями представля-ет собой единственный цикл в традиционной RAM-модели. Член |y| в sП(х) объясняет начальное пространство, взятое по входу.
Дополнения к базовой модели и вероятностные RAM-машины. Приводимые ниже результаты верны для RAM-машин, которые являются вероятностными в очень строгом смысле. А именно ЦП в этих машинах имеет доступ к случайным оракулам. Однако в предположении существования односторонних функций, случайные оракулы могут быть эффективно реализованы посредством псевдослучайных функций.
Для каждого k
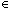
Всякий раз, когда машина входит в специальное состояние вызова оракула, содержимое оракульной ленты "только-для-чтения" изменяется мгновенно (т.е., за единственный шаг) и машина переходит к другому специальному состоянию. Строка, записанная на оракульной ленте "только-для-чтения" между двумя вызовами оракула называется запросом, соответствующим последнему вызову. Будем считать, что CPUk имеет доступ к функции f, если делается запрос q и оракул отвечает и изменяет содержимое оракульной ленты "только-для-чтения" на f(q). Вероятностная машина CPUk - это оракульная машина CPUk с доступом к однородно выбранной функции
f:{0,1}O(k) - > {0,1}.
Для каждого k
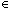
Повторные выполнения RAM-машины. Для решения проблемы защи-ты программ необходимо использовать повторные выполнения "одной и той же" RAM-программы на нескольких входах. Задача состоит в том, что RАМ-машина начинает следующее выполнение с рабочими лентами ЦП и МП, имеющих содержимое, идентичное их содержимому при окончании предыдущего выполнения программы.
Для каждого k
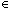
Эксперименты с RAM-машиной. Рассматриваются два типа противников. Оба могут неоднократно инициировать работу RAМ-машины на входах по своему выбору.
Различия между двумя типами противников состоит в их способности модифицировать коммуникационные ленты ЦП и МП в процессе вычислений. Вмешивающемуся противнику позволено как читать, так и записывать на эти ленты свою информацию (т.е., просматривать и изменять содержание взаимодействия), в то время как невмешивающемуся противнику позволено только читать эти ленты (то есть, только просматривать сообщения). В любом случае не надо позволять противнику иметь те же самые права доступа к рабочей ленте МП, так как содержимое этой ленты полностью определено начальным входом и сообщениями, посланными ЦП. Кроме того, в обоих случаях противник не имеет никакого доступа к внутренним лентам ЦП (т.е., к рабочим и оракульным лентам ЦП).
Для простоты, основное внимание будет уделяться противникам с экспоненциально ограниченным временем выполнения. Кроме того, время выполнения противника ограничено сверху 2n, где n - размер рабочей ленты ЦП. На практике противник будет ограничен по времени некоторым полиномом от длины рабочей ленты ЦП.
Невмешивающийся противник, обозначаемый как ADV является вероятностной машиной, которая на входе k и "шифрованной программе" ?, которая имеет следующий доступ к оракульной RAMk-машине. Машина ADV инициирует повторные выполнения RAMk-машины на входах по своему выбору до тех пор, пока общее время выполнения не стане равным 2k. В процессе каждого из этих выполнений, машина ADV имеет доступ "только-для-чтения" к коммуникационным лентам между CPUk и MEMk. Вмешивающийся противник определяется аналогично невмешивающемуся противнику за исключением того, что в процессе повторных вы-полнений противник имеет доступ для чтения и записи к коммуникацион-ным лентам между CPUk и МЕМk.
Преобразования, защищающие программное обеспечение
Определим компиляторы, которые по данной программе П, произво-дят пару (f,Пf), где f - случайно выбранная функция и Пf - "зашифрованная программа", которая соответствует П и f. Здесь имеется в виду оракульная RAM-машина, которая на входе (Пf,х) и при доступе к оракулу f моделирует выполнение П на данных х так, чтобы это моделирование "защищало бы" оригинальную программу П.
Далее даются определения компиляторов как набора преобразований программ в программно-оракульные пары, которые при выполнении оракульных RAM-программ являются функционально эквивалентными выполнениям оригинальных программ.
Компилятор, обозначаемый через C, является вероятностным отображением, которое по входу целочисленного параметра k и программы П для RAMk возвращает пару (f,Пf) так, чтобы
f:{0,1}O(k) - > {0,1} - случайно выбранная функция;
|Пf| =O(|П|);
Для k'=k+O(log k) существует оракульная RAMk'-машина такая, что для каждой П, каждой f и каждого x
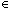
Оракульная RAMk'-машина отличается от RAMk-машины в том, что RAMk' имеет доступ к оракулу, в то время как RAMk нет. Понятно, что RAMk' имеет большую память, а именно RAMk'-машина состоит из 2k'=poly(k)2k слов, в то время как память RAMk состоит из 2k слов.
Компиляторы, как определено выше, преобразовывают детерминированные программы в "зашифрованные программы", которые выполняются на вероятностных RAM-машинах. Теперь непосредственно обратимся к определениям компилятора, защищающего программное обеспечение.
Оракул спецификации для программы П - это оракул, который на запрос x возвращает тройку (П(x),tП(x),sП(x)).
Отметим, что tП(x) и sП(x) обозначает время выполнения и пространственные размеры программы П на данных x. Далее даются основное определение для задачи защиты программ. В этом определении ADV может рассматриваться как вмешивающийся, так и невмешивающийся противник.
Для данного компилятора C и противника ADV, компилятор C защищает программное обеспечение против противника ADV, если существует вероятностная оракульная (в стандартном смысле) машина М, удовлетворяющая следующим условиям:
(М функционирует примерно за то же самое время, как и ADV): Существует полином p(') такой, что для каждой строки ? время выполнения М на входе (k', |?|) (и с учетом доступа к случайному оракулу) было ограничено p(k')T, где T обозначает время выполнения ADV при экспериментировании с RAMk' на входе ?.
(М с доступом к оракулу спецификации обеспечивает выход почти идентичный выходу ADV после экспериментирования с результатами работы компилятора): Для каждой программы П статистическое расстояние между следованием двух распределений вероятностей ограничено 2-k'.
Распределение выхода машины ADV при экспериментировании с RAMkf на входе Пf, где (f,Пf)< - C(П). Отметим, что RAMkf обозначает ин-терактивную пару (CPUk',MEMk'), где CPUk' имеет доступ к оракулу f. Распределение берется над пространством вероятностей, состоящим из всех возможных выборов функции f и всех возможных результатов выработки случайного бита ("подбрасываний монеты") машины ADV с равномерным распределением вероятностей.
Распределение выхода оракульной машины М на входе (k',O( П )) и при доступе к оракулу спецификации для П. Распределение берется над пространством вероятностей состоящим из всех возможных результатов подбрасываний монеты машины М с равномерным распределением вероятностей.
Компилятор C обеспечивает слабую защиту программ, если C защищает программы против любого невмешивающего противника. Компилятор C обеспечивает доказуемую защиту программ от вмешательства, если C защищает программы против любого вмешивающего противника.
Далее будет определяться затраты защиты программ. Необходимо напомнить, что для простоты, мы ограничиваем время выполнения программы П следующим условием: tП(x)> |П| + |x| для всех x.
Пусть C - компилятор и g:N - > N - некоторая целочисленная функция. Затраты компилятора C на большинстве аргументов g, если для каждой П, каждого x
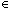
Определение забывающей RAM-машины и забывающего моделирования
Необходимо начать с определения модели доступа как последовательности ячеек памяти, к которым ЦП обращается в процессе вычислений. Это определение распространяется также на оракульный ЦП.
Модель доступа, обозначаемая как Аk(y) детерминированной RAMk-машины на входе y - это последовательность (a1,...,ai,...) такая, что для каждого i, i-тое сообщение, посланное CPUk при взаимодействии с MEMk(y) имеет форму (',ai,').
Теперь мы имеем дело с задачей забывающей сортировки n элементов посредством меток. Определяющее условие состоит в том, что RAM-машина, которая выполняет сортировку, может хранить только фиксированное число значений одновременно. Идея состоит в том, чтобы "выполнить" сортирующую сеть Батчера, который позволяет сортировать n элементов, выполняя n|log2n| 2 сравнений. Каждое сравнение "выполняется" посредством осуществления доступа к двум соответствующим словам, чтением их содержания и записью этих значений обратно в необходимом порядке. Последовательность операций доступа к памяти, сгенерированной для этой цели фиксирована и не зависит от входа. Отметим, что забывающая RAM-машина может легко вычислять в каждой точке, какое сравнение требуется для реализации следующего. Это следует из простой структуры сети Батчера, которая является однородной относительно логарифмического пространства. Этот алгоритм будет работать, если мы сохраняем метку каждого элемента вместе с самим элементом (виртуальное слово или макет).
Далее мы точно определим, как осуществить доступ к виртуальной ячейке или к макету i. Отметим, что после шага 1 виртуальные ячейки от 1 до m (также как и макеты от m+1 до m+
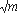
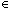 {1,...,m+
{1,...,m+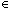
Далее описываются две альтернативных реализации шага 3. Первый вариант - реверсия модели доступа на шаге 2. Второй вариант - полная сортировка фактической памяти (то есть, все m+2
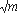
Первая сортировка выполняется в соответствии с ключом (v,? ), где v - виртуальный адрес (
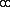
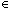 {0,1} указывает, исходит ли это слово из памяти зщт или из перемешанной памяти. Таким образом, сортируемый список имеет виртуальные адреса, появляющиеся так, чтобы некоторые из них появляются в двойном экземпляре, один за другим (одна версия из памяти зщт, а другая из перемешанной памяти). Затем, мы сканируем этот список и для каждого виртуального адреса, появляющегося в дубликате, маркируется второе местонахождение (возникающее из перемешанной памяти) также как и макет (т.е.,
{0,1} указывает, исходит ли это слово из памяти зщт или из перемешанной памяти. Таким образом, сортируемый список имеет виртуальные адреса, появляющиеся так, чтобы некоторые из них появляются в двойном экземпляре, один за другим (одна версия из памяти зщт, а другая из перемешанной памяти). Затем, мы сканируем этот список и для каждого виртуального адреса, появляющегося в дубликате, маркируется второе местонахождение (возникающее из перемешанной памяти) также как и макет (т.е., 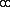
Далее следует детальное описание шага 2. Главная идея при этом моделировании состоит в том, чтобы осуществить доступ к каждой виртуальной ячейке в "перемешанной памяти" только в течение каждого шага периода. Как только "осуществиться" доступ к некоторой виртуальной ячейке, необходимо сохранить версию этой виртуальной ячейке в памяти зщт. В течение шага 2, счт содержит число виртуальных операций доступа, моделируемых в текущем периоде. Переменная счт - первоначально содержит 0 и увеличивается, пока достигнет значения
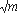
(2a) сканирует полностью память зщт и ищет виртуальный адрес i. А именно, для j, пробегающему значения от m+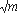
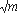 , доступ к фактической ячейке памяти j переменная found устанавливается в true и сохраняется в ЦП, если виртуальный адрес i совпадает с фактической ячейкой j. (Переменная found инициализирована в значение false до этого сканирования и остается такой же, если виртуальный адрес i не был найден);
, доступ к фактической ячейке памяти j переменная found устанавливается в true и сохраняется в ЦП, если виртуальный адрес i совпадает с фактической ячейкой j. (Переменная found инициализирована в значение false до этого сканирования и остается такой же, если виртуальный адрес i не был найден);
(2b) если found=false, тогда забывающая RAM-машина осуществляет доступ к слову с меткой ?(i) и сохраняет содержимое в ЦП. Как показано выше, это реализуется посредство двоичного поиска метки ?(i);
(2c) если found=true, тогда забывающая RAM-машина осуществляет доступ к слову с меткой ?(m+счт), которое является "макетом". Это также реализуется посредством двоичного поиска метки ?(m+счт);
(2d) просматривает полностью память зщт снова и записывает модифицируемое значение i-того виртуального слова в памяти зщт. А именно, для m+
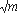
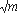 доступ к фактической ячейке памяти j запоминается в ее модифицированном значении виртуального адреса i, если адрес j содержит старое значение виртуального адреса i (т.е., found=true), либо found=false и j - первое пустое слово в shelter-е.
доступ к фактической ячейке памяти j запоминается в ее модифицированном значении виртуального адреса i, если адрес j содержит старое значение виртуального адреса i (т.е., found=true), либо found=false и j - первое пустое слово в shelter-е. Значение счт увеличивается на 1.
Подчеркнем, что наблюдатель не может видеть, сохранил ли ЦП значения или нет и, таким образом, не может различать выполнение шага 2b от выполнения шага 2c. Ясно, что шаги 2a и 2d имеют фиксированную модель доступа и, таким образом, не никакая информация, полезная для наблюдателя, не вскрывается.
Анализ алгоритма "Квадратного корня"
Как обсуждалось выше, последовательность фактических операций доступа к памяти забывающей RAM-машины действительно не открывает никакой информации относительно последовательности виртуальных операций доступа к памяти оригинальной RAM-машины. Это действительно так, потому что во время шагов 1, 2a, 2d и 3 фактическая модель доступа фиксирована, в то время как во время шагов 2b и 2c фактические модели доступа неразличимы и "случайны".
Теперь остается вычислить затраты на моделирование (т.е., отношение числа операций доступа, выполненных на забывающей RAM-машиной к числу оригинальных операций доступа). Далее мы вычисляем общее число фактических операций доступа, выполняемых на период (т.е., m+2
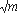
То же самое делается на шаге 3. Что касается шага 2, каждая виртуальная операция доступа выполняется за 2
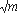
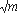 )=O(
)=O(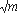
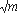 ). Фактически, вышеупомянутый выбор параметров (то есть, размер памяти зщт) не оптимален.
). Фактически, вышеупомянутый выбор параметров (то есть, размер памяти зщт) не оптимален. При использовании памяти зщт размера s, мы получаем амортизационные затраты
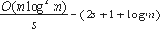
которые минимизированы установкой s=?(logm
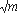
Заключительные замечания
В данном подразделе был представлен компилятор, который трансформировал RAM-программы в эквивалентные программы, которые предотвращают попытки противника выяснить что-либо относительно этих программ при их выполнении. Перенос был выполнен на уровне команд, а именно операции доступа к памяти для каждой команды заменялись последовательностью избыточных операций доступа к памяти. Понятно, что все формулировки и результаты, показанные выше, применимы к любому другому уровню детализации выполнения программ. Например, на уровне "пролистывания" памяти это означало бы, что мы имеем дело с операциями "получить страницу" и "сохранить страницу", как с атомарными (базовыми) командами доступа. Таким образом, единственная операция "доступ к странице" заменяется последовательностью избыточных операций "доступ к странице". В целом исследуется механизм для забывающего доступа к большому количеству незащищенных ячеек памяти при использовании ограниченного защищенного участка памяти. Применение к защите программ было единственным приложением, обсужденным выше, но возможны также и другие приложения.
Одно возможное приложение - это управление распределенными базами данных в сети доверенных сайтов, связанных небезопасными каналами. Например, если в сети сайтов нет ни одного, который содержал бы полную базу данных, значит необходимо распределить всю база данных среди этих сайтов. Пользователи соединяются с сайтами так, чтобы можно было восстановить информацию из базы данных таким образом, чтобы не позволить противнику (который контролирует каналы) изучить какая часть базы данных является наиболее используемой или, вообще, узнать модель доступа любого пользователя.
В данном случае не требуется скрывать факт, что запрос к базе данных был выполнен некоторым сайтом в некоторое время, - просто надо скрывать любую информацию в отношении фрагмента необходимых данных. Также принимается предположение о том, что запросы пользователей выполняются "один за другим", а не параллельно. Легко увидеть, что забывающее моделирование RAM-машины может применяться к этому приложению посредством ассоциирования сайтов с ячейками памяти. Роль центрального процессора будет играть сайт, который в текущий момент времени запрашивает данные из базы и информация о моделировании может циркулировать между сайтами забывающим способом. Отметим, что вышеупомянутое приложение отличается из традиционной задачи анализа трафика.
Другое приложение - это задача контроль структуры данных, которая следует из определений самотестирующихся программ, рассматриваемых выше. В этой конструкции желательно сохранить структуру данных при использовании малого количества достоверной памяти. Большая часть структуры данных может сохраняться в незащищенной памяти, где и надо решать задачу защиты от вмешательства противника. Цель состоит в том, как обеспечить механизм контроля целостности данных, которые необходимо сохранять посредством забывающего моделирования RAM-машиной.